Учёные вывели формулу успеха научных статей
Это звучит, как мечта научного администратора или худший кошмар учёного: вычислена формула, способная прогнозировать, как часто будет цитироваться та или иная научная статья. Команда учёных из США сообщает, что простая модель позволяет делать достаточно точные прогнозы будущих упоминаний научных статей в СМИ на основе базы данных, собранной в течение примерно пяти последних лет.
"Нам бы хотелось предсказывать как можно раньше и точнее, какие именно статьи покажутся впечатляющими и важными для аудитории, – рассказывает один из авторов исследования, Дашунь Ван (Dashun Wang) из исследовательского центра Томаса Уотсона в Нью-Йорке (IBM).
Математическая модель прогнозирования опирается на ключевые слова, по которым статья цитируется в первые годы после публикации. Удивительно, но модели не нужно знать даже автора, предмет статьи или журнал, в котором она была впервые опубликована.
Вместо этого создатели предположили, что на популярность статьи влияют всего три фактора. Первый – это, разумеется, привлекательность самой идеи. Второй фактор — становится ли статья цитируемой сразу после выхода (это способно сделать её ещё более популярной, срабатывает сетевой эффект, делающий известное ещё известнее). Третий фактор — это новизна информации. Когда она исчезает, цитирование статьи постепенно спадает до нуля.
Совместно с Альбертом-Ласло Барабази (Albert-László Barabási), сетевым теоретиком из Северо-Восточного университета, и Чаомин Сон (Chaoming Song), физиком из университета Майами, Ван построил модель, учитывающую все три фактора с математической поправкой на актуальность.
На выходе она выдаёт универсальную кривую, которая иллюстрирует скорость роста популярности и спада интереса к научной работе. С небольшими погрешностями модель может прогнозировать диапазон влияния будущей статьи и наиболее вероятные цитаты из неё.
Исследователи проверили свою модель на научных работах по физике, опубликованных с 1960-х годов. Их прогнозы основывались на пятилетней базе цитирования. Они обнаружили, что спустя 25 лет цитирование 93,5% работ снижается согласно их прогнозам.
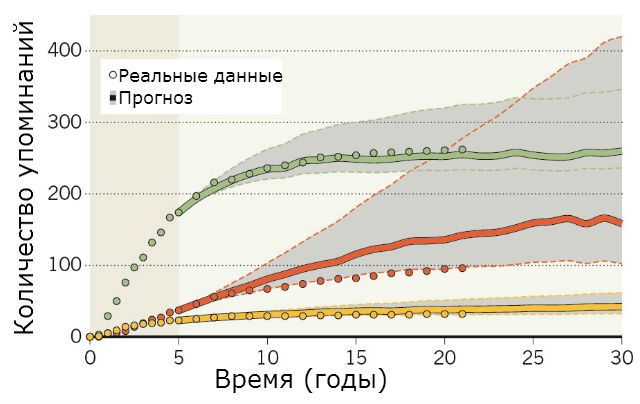
По мнению Вана, прогнозы могут быть сделаны на основе данных, собранных и менее чем за 5 лет, поскольку пик цитирования приходится примерно на первые два года после выхода статьи, а затем популярность постепенно угасает.
Математическая модель применима также и к статьям 1990-х и 2000-х годов. Однако, 6,5% статей полностью опровергают результаты прогноза: некоторые работы не получали известность или уважение в течение первых пяти лет после публикации, но затем внезапно словно обретали "второе дыхание" и становились весьма влиятельными в научной сфере.
Учёные, не принимавшие участия в данном исследовании, но работающие в той же сфере, похвалили модель команды Вана. Однако они же высказали мнение, что прогнозирование влияния статьи спустя пять лет после её публикации практически не имеет смысла. К тому же, следует понимать, что популярность статей неизбежно разнится в зависимости от сферы деятельности учёного. То есть биологи всегда будут цитировать друг друга больше, чем физиков.
В будущем Ван планирует усовершенствовать свою модель, введя в неё более сложные элементы – такие, как тема статьи или место публикации.
"Сейчас мы учитывали лишь малозначимые факторы. Удивительно, что удалось достичь такого уровня предсказуемости, учитывая лишь статистику цитирования с течением времени", – говорит он.
Ван и его коллеги также добавляют, что модель можно использовать и для прогнозирования будущего сразу нескольких публикаций. Например, всех работ, опубликованных в одном журнале, одним институтом или под руководством одного конкретного учёного. Так что в какой-то степени даже индивидуальная карьера научного сотрудника вскоре будет предсказуемой.
В ближайшее время группа Вана надеется создать сайт, который сможет выдавать прогноз цитирования для любой научной работы.
Также по теме:
Успех блокбастеров предскажет математическая модель
Наука должна производить. Эфир программы "Наука 2.0"
Открытие ученых: миром правит одна сверхкорпорация
Проверить алгеброй московские пробки





















